Please provide your feedback about the website at feedback@apc.iisc.ernet.in
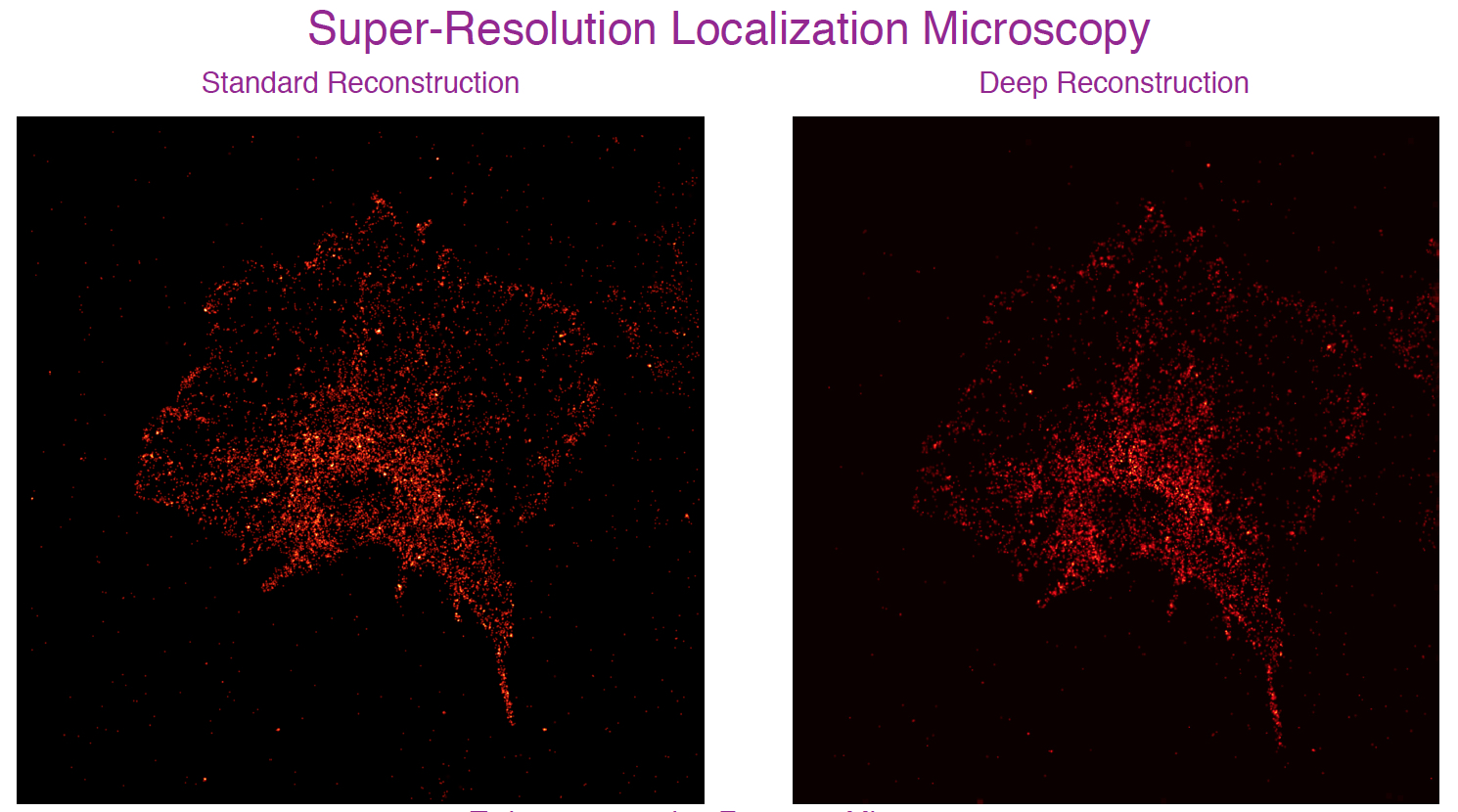
We address the problem of sparse spike deconvolution from noisy measurements within a Bayesian paradigm that incorporates sparsity promoting priors about the ground truth. The optimization problem arising out of this formulation warrants an iterative solution. A typical iterative algorithm includes an affine transformation and a nonlinear thresholding step. Effectively, a cascade/sequence of affine and nonlinear transformations gives rise to the reconstruction. This is also the structure in a typical deep neural network (DNN). This observation establishes the link between inverse problems and deep neural networks. The architecture of the DNN is such that the weights and biases in each layer are fixed and determined by the blur matrix/sensing matrix and the noisy measurements, and the sparsity promoting prior determines the activation function in each layer. In scenarios where the priors are not available exactly, but adequate training data is available, the formulation can be adapted to learn the priors by parameterizing the activation function using a linear expansion of threshold (LET) functions. As a proof of concept, we demonstrated successful spike deconvolution on synthetic dataset and showed significant advantages over standard reconstruction approaches such as the fast iterative shrinkage-thresholding algorithm (FISTA). We also show an application of the proposed method for performing image reconstruction in super-resolution localization microscopy. Effectively, this is a deconvolution problem and we refer to the resulting DNNs as Bayesian Deep Deconvolutional Networks.
Once a DNN based solution to the sparse coding problem is available, one can use it to also perform dictionary learning.
