Online Reconstruction Algorithms for Compressed Imaging

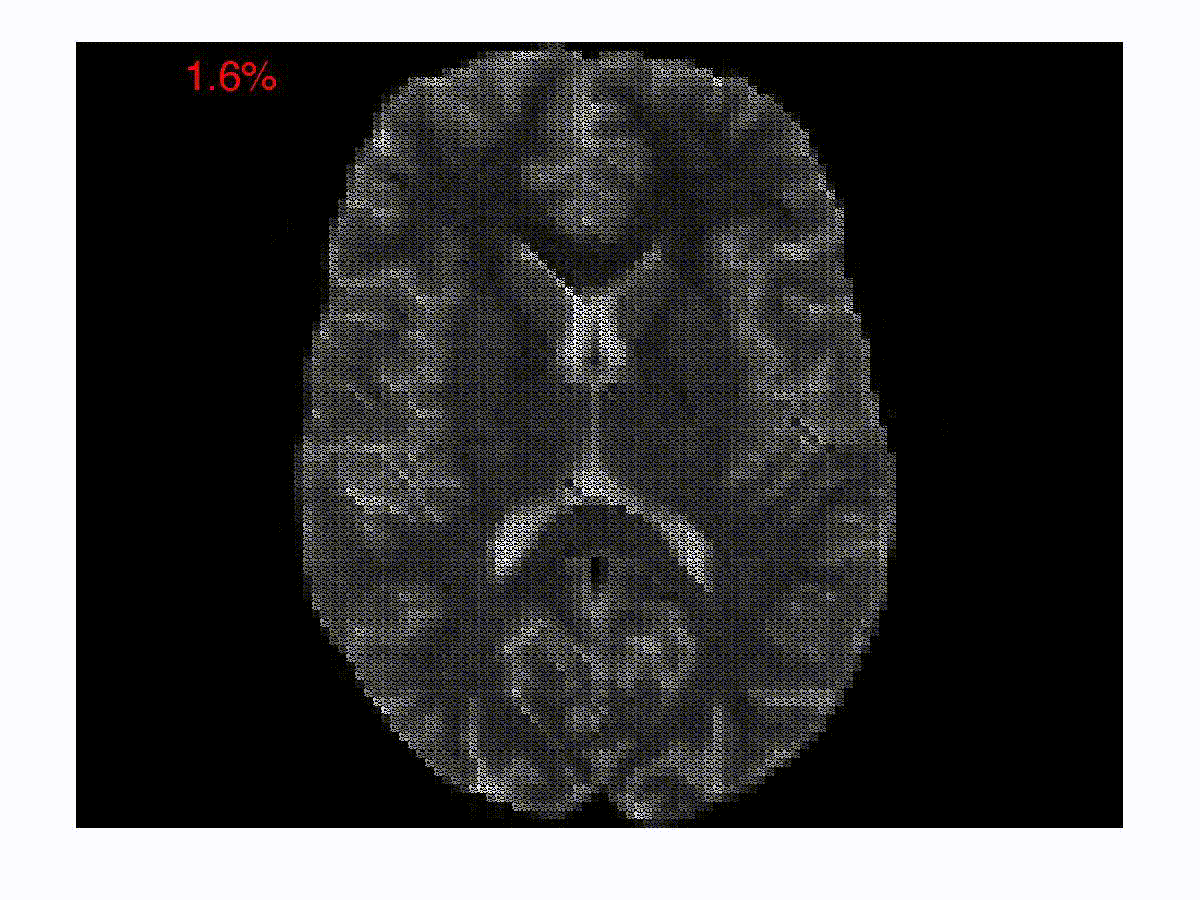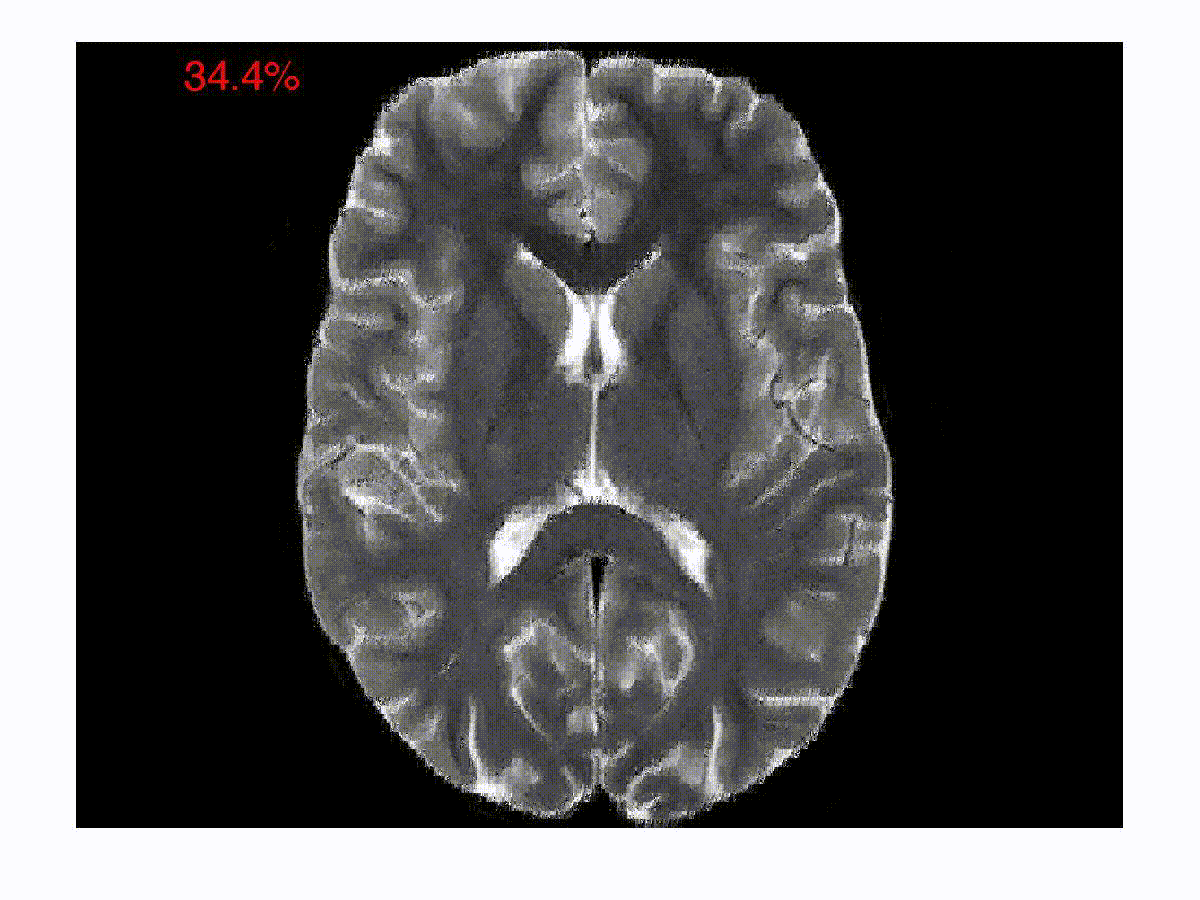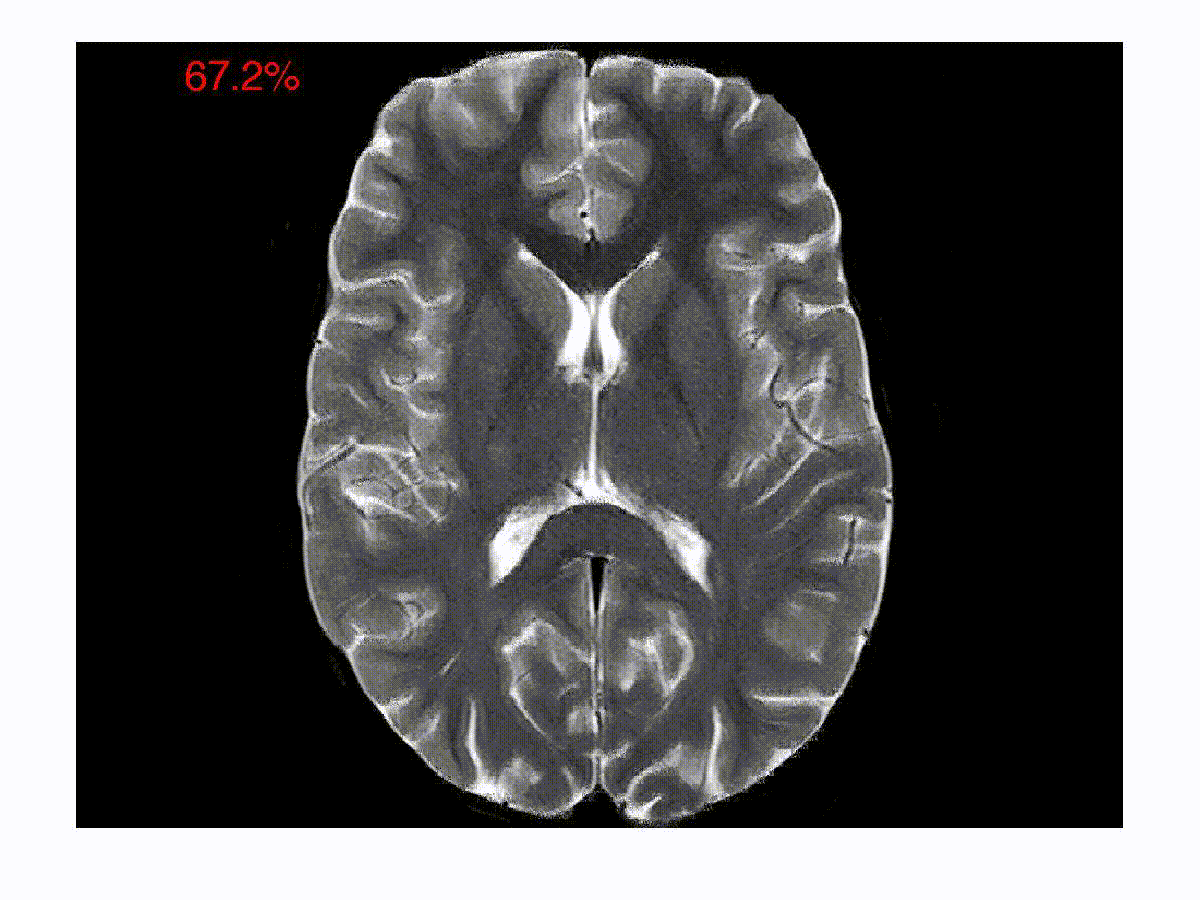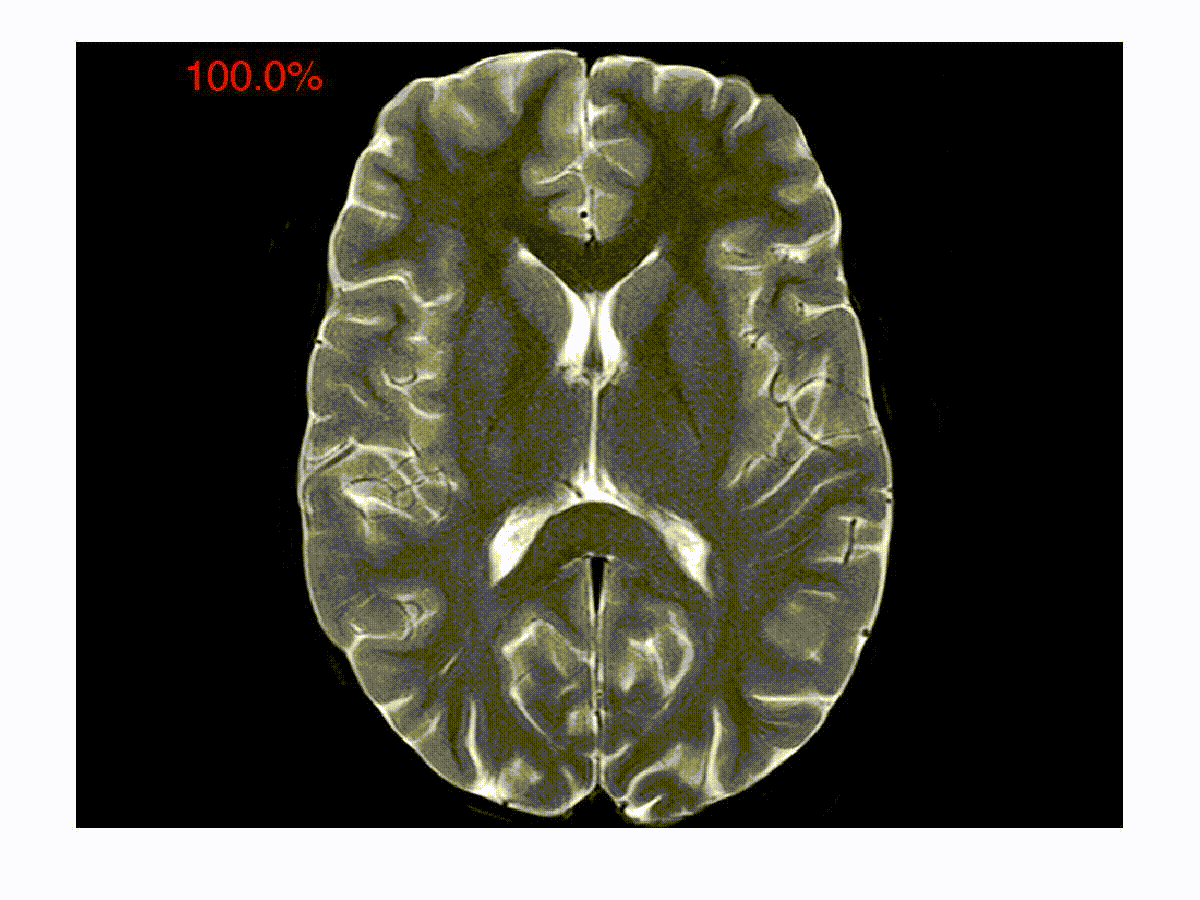
One of the focus areas of the Spectrum Lab is in solving inverse problems in imaging and image processing. In a typical compressed imaging application, one acquires projections of a scene on to random test/sensing vectors, which are often binary. In an optical imaging setup, a binary sensing array is essentially an amplitude mask that allows light to go through in some regions and blocks light in the other regions. In a magnetic resonance imaging setup, the sensing vectors are two-dimensional Fourier vectors. The goal in these new imaging modalities is to reconstruct the images from the compressed/encoded measurements. The compression in such a setup happens right at the level of acquisition. The goal is to develop computationally efficient online decoding techniques that sequentially update the reconstruction as the measurements arrive. The reconstruction technique also incorporates priors about the underlying image such as sparsity in an appropriate basis. Such a sequential reconstruction scheme has the advantage that one can stop acquiring measurements as and when the reconstructed image meets a certain objective or subjective quality requirement. We have developed low-complexity online reconstruction techniques that are on par with batch-mode reconstruction techniques in terms of the quality of reconstruction. The images show the reconstructions as the measurements are revealed sequentially. We are currently developing Deep Neural Network (DNN) based image reconstruction schemes that can be fine-tuned to maximize the reconstruction quality for specific imaging settings.